ESTATÍSTICA INFERENCIAL
Na equação de regressão múltipla y = β0 + β1x1 + β2x2 + β3x3 + ε, como você testaria a hipótese conjunta β1 = β2 = β3?
Comparando o valor da estatística t de teste com o valor da estatística t crítico do coeficiente β1: se t teste for maior que t crítico, não rejeitaria a hipótese de que β1 é igual a zero e concluiria que a igualdade β1 = β2 = β3 é válida.
Verificando o valor do coeficiente de determinação múltipla: rejeitaria a hipótese β1 = β2 = β3 se o coeficiente de determinação múltipla fosse menor que 1.
Comparando o valor da estatística F teste com o valor da estatística F crítico: se F teste for maior que F crítico, rejeitaria a hipótese β1 = β2 = β3 .
Comparando o valor da estatística t de teste com o valor da estatística t crítico do coeficiente β2: se t teste for maior que t crítico, não rejeitaria a hipótese de que β2 é igual a zero e concluiria que a igualdade β1 = β2 = β3 é válida.
Verificando o valor do coeficiente de determinação múltipla: não rejeitaria a hipótese β1 = β2 = β3 se o coeficiente de determinação múltipla fosse maior que 1.
O modelo de regressão linear simples a seguir, estimado a partir dos dados coletados em 23 dias de observação, descreve as quantidades de quilogramas de banana nanica vendidas diariamente em um supermercado, y, como função de seu preço (R$/kg) x.
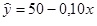
Considere ainda as seguintes estatísticas:
- Coeficiente de determinação: 0,863.
- Estatística F crítica, para 5% de significância e (1; 21) graus de liberdade = 4,32.
- Estatística F de teste = 2,57.
Com base nessas informações, julgue as seguintes afirmações a respeito do modelo estimado.
I. O modelo mostra que há uma relação inversa entre preço e quantidade vendida.
II. Se o preço da banana for R$ 3,90/kg, espera-se que sejam vendidos 49,6 kg/dia.
III. As quantidades vendidas explicam 86,3% das variações no preço da banana.
IV. O teste de hipóteses permite concluir que o modelo é significante, logo, o preço da banana explica a quantidade vendida de banana.
Estão corretas as afirmações:
I e II, somente.
I e III, somente.
I, II e III, somente.
II e III, somente.
I, II, III e IV.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 321.)
O gerente de uma revenda de automóveis está concebendo um novo plano de gratificações para aumentar o volume de vendas. Atualmente, o volume médio de vendas é de 14 automóveis por mês. O gerente quer realizar uma pesquisa para ver se o novo plano de gratificações aumentará o volume de vendas. Para coletar dados sobre o plano, uma amostra do pessoal de vendas terá permissão de realizar vendas sob o novo plano de gratificações por um período de um mês.
Que forma de hipóteses deve ser usada para testar o plano do gerente?
Ho: µ ≥ 14 automóveis; Ha: µ < 14 automóveis.
Ho: µ ≤ 14 automóveis; Ha: µ > 14 automóveis.
Ho: µ = 14 automóveis; Ha: µ ≠ 14 automóveis.
Ho: µ < 14 automóveis; Ha: µ ≥ 14 automóveis.
Ho: µ > 14 automóveis; Ho: µ ≤ 14 automóveis.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual do desvio padrão das notas da disciplina Matemática Básica? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
Dado adicional:
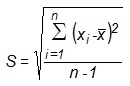
1,19 pontos.
1,22 pontos.
1,24 pontos.
1,16 pontos.
1,14 pontos.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 306.).
Os dados de perfil de audiência coletados no web site da ESPN Sportszone mostraram que 26% dos usuários eram mulheres (USA Today, 20 de janeiro de 1998). Considere que essa porcentagem foi baseada numa amostra de 400 usuários. Com uma confiança de 95%, qual a margem de erro associada com a proporção estimada de usuários que são mulheres? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96

± 5,68%.
± 2,86%.
± 3,56%.
± 1,56%.
± 4,30%.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual da média final da disciplina Matemática Básica?
7,82.
4,92.
6,42.
6,87.
8,22.
Em uma equação de regressão envolvendo 30 observações, foi obtida a seguinte equação de regressão estimada:
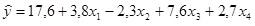
Qual o valor estimado de y quando x1 = 10, x2 = 5, x3 = 1 e x4 = 2? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
80,20.
32,40.
102,30.
48,90.
57,10.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 459.
O gerente de recursos humanos de uma empresa de tecnologia da informação reuniu dados sobre as notas obtidas nos programas de treinamento e salários mensais dos colaboradores. Foi estimada a equação de regressão
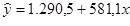
em que x = salários mensais; y = média das notas, encontrando-se os seguintes valores:
Coeficiente de determinação r2 = 0,746;
Fcrítico = 5,96
Fteste = 11,7.
A respeito desse modelo, julgue as seguintes afirmações:
I. Os salários mensais são a variável explicativa e as notas são a variável explicada.
II. As notas obtidas no programa de treinamento explicam 74,6% das variações observadas nos salários mensais.
III. No teste de hipóteses sobre a validade do modelo, rejeita-se a hipótese nula e conclui-se que as notas explicam os salários mensais.
IV. Para cada 1 ponto adicional nos salários mensais, espera-se um acréscimo de R$ 581,10 nas médias das notas.
Estão corretas as afirmações:
II, III e IV, apenas.
I e IV, apenas.
I, II e III, apenas.
I, III e IV, apenas.
I, II, III, IV.

Comparando o valor da estatística t de teste com o valor da estatística t crítico do coeficiente β1: se t teste for maior que t crítico, não rejeitaria a hipótese de que β1 é igual a zero e concluiria que a igualdade β1 = β2 = β3 é válida.
Verificando o valor do coeficiente de determinação múltipla: rejeitaria a hipótese β1 = β2 = β3 se o coeficiente de determinação múltipla fosse menor que 1.
Comparando o valor da estatística F teste com o valor da estatística F crítico: se F teste for maior que F crítico, rejeitaria a hipótese β1 = β2 = β3 .
Comparando o valor da estatística t de teste com o valor da estatística t crítico do coeficiente β2: se t teste for maior que t crítico, não rejeitaria a hipótese de que β2 é igual a zero e concluiria que a igualdade β1 = β2 = β3 é válida.
Verificando o valor do coeficiente de determinação múltipla: não rejeitaria a hipótese β1 = β2 = β3 se o coeficiente de determinação múltipla fosse maior que 1.
O modelo de regressão linear simples a seguir, estimado a partir dos dados coletados em 23 dias de observação, descreve as quantidades de quilogramas de banana nanica vendidas diariamente em um supermercado, y, como função de seu preço (R$/kg) x.
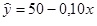
Considere ainda as seguintes estatísticas:
- Coeficiente de determinação: 0,863.
- Estatística F crítica, para 5% de significância e (1; 21) graus de liberdade = 4,32.
- Estatística F de teste = 2,57.
Com base nessas informações, julgue as seguintes afirmações a respeito do modelo estimado.
I. O modelo mostra que há uma relação inversa entre preço e quantidade vendida.
II. Se o preço da banana for R$ 3,90/kg, espera-se que sejam vendidos 49,6 kg/dia.
III. As quantidades vendidas explicam 86,3% das variações no preço da banana.
IV. O teste de hipóteses permite concluir que o modelo é significante, logo, o preço da banana explica a quantidade vendida de banana.
Estão corretas as afirmações:
I e II, somente.
I e III, somente.
I, II e III, somente.
II e III, somente.
I, II, III e IV.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 321.)
O gerente de uma revenda de automóveis está concebendo um novo plano de gratificações para aumentar o volume de vendas. Atualmente, o volume médio de vendas é de 14 automóveis por mês. O gerente quer realizar uma pesquisa para ver se o novo plano de gratificações aumentará o volume de vendas. Para coletar dados sobre o plano, uma amostra do pessoal de vendas terá permissão de realizar vendas sob o novo plano de gratificações por um período de um mês.
Que forma de hipóteses deve ser usada para testar o plano do gerente?
Ho: µ ≥ 14 automóveis; Ha: µ < 14 automóveis.
Ho: µ ≤ 14 automóveis; Ha: µ > 14 automóveis.
Ho: µ = 14 automóveis; Ha: µ ≠ 14 automóveis.
Ho: µ < 14 automóveis; Ha: µ ≥ 14 automóveis.
Ho: µ > 14 automóveis; Ho: µ ≤ 14 automóveis.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual do desvio padrão das notas da disciplina Matemática Básica? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
Dado adicional:
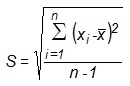
1,19 pontos.
1,22 pontos.
1,24 pontos.
1,16 pontos.
1,14 pontos.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 306.).
Os dados de perfil de audiência coletados no web site da ESPN Sportszone mostraram que 26% dos usuários eram mulheres (USA Today, 20 de janeiro de 1998). Considere que essa porcentagem foi baseada numa amostra de 400 usuários. Com uma confiança de 95%, qual a margem de erro associada com a proporção estimada de usuários que são mulheres? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96

± 5,68%.
± 2,86%.
± 3,56%.
± 1,56%.
± 4,30%.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual da média final da disciplina Matemática Básica?
7,82.
4,92.
6,42.
6,87.
8,22.
Em uma equação de regressão envolvendo 30 observações, foi obtida a seguinte equação de regressão estimada:
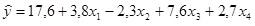
Qual o valor estimado de y quando x1 = 10, x2 = 5, x3 = 1 e x4 = 2? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
80,20.
32,40.
102,30.
48,90.
57,10.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 459.
O gerente de recursos humanos de uma empresa de tecnologia da informação reuniu dados sobre as notas obtidas nos programas de treinamento e salários mensais dos colaboradores. Foi estimada a equação de regressão
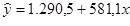
em que x = salários mensais; y = média das notas, encontrando-se os seguintes valores:
Coeficiente de determinação r2 = 0,746;
Fcrítico = 5,96
Fteste = 11,7.
A respeito desse modelo, julgue as seguintes afirmações:
I. Os salários mensais são a variável explicativa e as notas são a variável explicada.
II. As notas obtidas no programa de treinamento explicam 74,6% das variações observadas nos salários mensais.
III. No teste de hipóteses sobre a validade do modelo, rejeita-se a hipótese nula e conclui-se que as notas explicam os salários mensais.
IV. Para cada 1 ponto adicional nos salários mensais, espera-se um acréscimo de R$ 581,10 nas médias das notas.
Estão corretas as afirmações:
II, III e IV, apenas.
I e IV, apenas.
I, II e III, apenas.
I, III e IV, apenas.
I, II, III, IV.

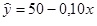
I e II, somente.
I e III, somente.
I, II e III, somente.
II e III, somente.
I, II, III e IV.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 321.)
O gerente de uma revenda de automóveis está concebendo um novo plano de gratificações para aumentar o volume de vendas. Atualmente, o volume médio de vendas é de 14 automóveis por mês. O gerente quer realizar uma pesquisa para ver se o novo plano de gratificações aumentará o volume de vendas. Para coletar dados sobre o plano, uma amostra do pessoal de vendas terá permissão de realizar vendas sob o novo plano de gratificações por um período de um mês.
Que forma de hipóteses deve ser usada para testar o plano do gerente?
Ho: µ ≥ 14 automóveis; Ha: µ < 14 automóveis.
Ho: µ ≤ 14 automóveis; Ha: µ > 14 automóveis.
Ho: µ = 14 automóveis; Ha: µ ≠ 14 automóveis.
Ho: µ < 14 automóveis; Ha: µ ≥ 14 automóveis.
Ho: µ > 14 automóveis; Ho: µ ≤ 14 automóveis.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual do desvio padrão das notas da disciplina Matemática Básica? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
Dado adicional:
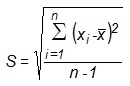
1,19 pontos.
1,22 pontos.
1,24 pontos.
1,16 pontos.
1,14 pontos.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 306.).
Os dados de perfil de audiência coletados no web site da ESPN Sportszone mostraram que 26% dos usuários eram mulheres (USA Today, 20 de janeiro de 1998). Considere que essa porcentagem foi baseada numa amostra de 400 usuários. Com uma confiança de 95%, qual a margem de erro associada com a proporção estimada de usuários que são mulheres? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96

± 5,68%.
± 2,86%.
± 3,56%.
± 1,56%.
± 4,30%.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual da média final da disciplina Matemática Básica?
7,82.
4,92.
6,42.
6,87.
8,22.
Em uma equação de regressão envolvendo 30 observações, foi obtida a seguinte equação de regressão estimada:
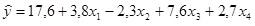
Qual o valor estimado de y quando x1 = 10, x2 = 5, x3 = 1 e x4 = 2? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
80,20.
32,40.
102,30.
48,90.
57,10.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 459.
O gerente de recursos humanos de uma empresa de tecnologia da informação reuniu dados sobre as notas obtidas nos programas de treinamento e salários mensais dos colaboradores. Foi estimada a equação de regressão
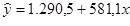
em que x = salários mensais; y = média das notas, encontrando-se os seguintes valores:
Coeficiente de determinação r2 = 0,746;
Fcrítico = 5,96
Fteste = 11,7.
A respeito desse modelo, julgue as seguintes afirmações:
I. Os salários mensais são a variável explicativa e as notas são a variável explicada.
II. As notas obtidas no programa de treinamento explicam 74,6% das variações observadas nos salários mensais.
III. No teste de hipóteses sobre a validade do modelo, rejeita-se a hipótese nula e conclui-se que as notas explicam os salários mensais.
IV. Para cada 1 ponto adicional nos salários mensais, espera-se um acréscimo de R$ 581,10 nas médias das notas.
Estão corretas as afirmações:
II, III e IV, apenas.
I e IV, apenas.
I, II e III, apenas.
I, III e IV, apenas.
I, II, III, IV.

Ho: µ ≥ 14 automóveis; Ha: µ < 14 automóveis.
Ho: µ ≤ 14 automóveis; Ha: µ > 14 automóveis.
Ho: µ = 14 automóveis; Ha: µ ≠ 14 automóveis.
Ho: µ < 14 automóveis; Ha: µ ≥ 14 automóveis.
Ho: µ > 14 automóveis; Ho: µ ≤ 14 automóveis.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual do desvio padrão das notas da disciplina Matemática Básica? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
Dado adicional:
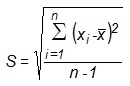
1,19 pontos.
1,22 pontos.
1,24 pontos.
1,16 pontos.
1,14 pontos.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 306.).
Os dados de perfil de audiência coletados no web site da ESPN Sportszone mostraram que 26% dos usuários eram mulheres (USA Today, 20 de janeiro de 1998). Considere que essa porcentagem foi baseada numa amostra de 400 usuários. Com uma confiança de 95%, qual a margem de erro associada com a proporção estimada de usuários que são mulheres? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96

± 5,68%.
± 2,86%.
± 3,56%.
± 1,56%.
± 4,30%.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual da média final da disciplina Matemática Básica?
7,82.
4,92.
6,42.
6,87.
8,22.
Em uma equação de regressão envolvendo 30 observações, foi obtida a seguinte equação de regressão estimada:
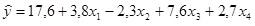
Qual o valor estimado de y quando x1 = 10, x2 = 5, x3 = 1 e x4 = 2? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
80,20.
32,40.
102,30.
48,90.
57,10.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 459.
O gerente de recursos humanos de uma empresa de tecnologia da informação reuniu dados sobre as notas obtidas nos programas de treinamento e salários mensais dos colaboradores. Foi estimada a equação de regressão
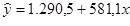
em que x = salários mensais; y = média das notas, encontrando-se os seguintes valores:
Coeficiente de determinação r2 = 0,746;
Fcrítico = 5,96
Fteste = 11,7.
A respeito desse modelo, julgue as seguintes afirmações:
I. Os salários mensais são a variável explicativa e as notas são a variável explicada.
II. As notas obtidas no programa de treinamento explicam 74,6% das variações observadas nos salários mensais.
III. No teste de hipóteses sobre a validade do modelo, rejeita-se a hipótese nula e conclui-se que as notas explicam os salários mensais.
IV. Para cada 1 ponto adicional nos salários mensais, espera-se um acréscimo de R$ 581,10 nas médias das notas.
Estão corretas as afirmações:
II, III e IV, apenas.
I e IV, apenas.
I, II e III, apenas.
I, III e IV, apenas.
I, II, III, IV.

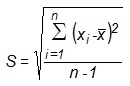
1,19 pontos.
1,22 pontos.
1,24 pontos.
1,16 pontos.
1,14 pontos.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 306.).
Os dados de perfil de audiência coletados no web site da ESPN Sportszone mostraram que 26% dos usuários eram mulheres (USA Today, 20 de janeiro de 1998). Considere que essa porcentagem foi baseada numa amostra de 400 usuários. Com uma confiança de 95%, qual a margem de erro associada com a proporção estimada de usuários que são mulheres? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96

± 5,68%.
± 2,86%.
± 3,56%.
± 1,56%.
± 4,30%.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual da média final da disciplina Matemática Básica?
7,82.
4,92.
6,42.
6,87.
8,22.
Em uma equação de regressão envolvendo 30 observações, foi obtida a seguinte equação de regressão estimada:
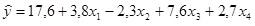
Qual o valor estimado de y quando x1 = 10, x2 = 5, x3 = 1 e x4 = 2? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
80,20.
32,40.
102,30.
48,90.
57,10.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 459.
O gerente de recursos humanos de uma empresa de tecnologia da informação reuniu dados sobre as notas obtidas nos programas de treinamento e salários mensais dos colaboradores. Foi estimada a equação de regressão
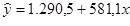
em que x = salários mensais; y = média das notas, encontrando-se os seguintes valores:
Coeficiente de determinação r2 = 0,746;
Fcrítico = 5,96
Fteste = 11,7.
A respeito desse modelo, julgue as seguintes afirmações:
I. Os salários mensais são a variável explicativa e as notas são a variável explicada.
II. As notas obtidas no programa de treinamento explicam 74,6% das variações observadas nos salários mensais.
III. No teste de hipóteses sobre a validade do modelo, rejeita-se a hipótese nula e conclui-se que as notas explicam os salários mensais.
IV. Para cada 1 ponto adicional nos salários mensais, espera-se um acréscimo de R$ 581,10 nas médias das notas.
Estão corretas as afirmações:
II, III e IV, apenas.
I e IV, apenas.
I, II e III, apenas.
I, III e IV, apenas.
I, II, III, IV.


± 5,68%.
± 2,86%.
± 3,56%.
± 1,56%.
± 4,30%.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual da média final da disciplina Matemática Básica?
7,82.
4,92.
6,42.
6,87.
8,22.
Em uma equação de regressão envolvendo 30 observações, foi obtida a seguinte equação de regressão estimada:
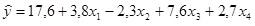
Qual o valor estimado de y quando x1 = 10, x2 = 5, x3 = 1 e x4 = 2? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
80,20.
32,40.
102,30.
48,90.
57,10.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 459.
O gerente de recursos humanos de uma empresa de tecnologia da informação reuniu dados sobre as notas obtidas nos programas de treinamento e salários mensais dos colaboradores. Foi estimada a equação de regressão
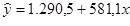
em que x = salários mensais; y = média das notas, encontrando-se os seguintes valores:
Coeficiente de determinação r2 = 0,746;
Fcrítico = 5,96
Fteste = 11,7.
A respeito desse modelo, julgue as seguintes afirmações:
I. Os salários mensais são a variável explicativa e as notas são a variável explicada.
II. As notas obtidas no programa de treinamento explicam 74,6% das variações observadas nos salários mensais.
III. No teste de hipóteses sobre a validade do modelo, rejeita-se a hipótese nula e conclui-se que as notas explicam os salários mensais.
IV. Para cada 1 ponto adicional nos salários mensais, espera-se um acréscimo de R$ 581,10 nas médias das notas.
Estão corretas as afirmações:
II, III e IV, apenas.
I e IV, apenas.
I, II e III, apenas.
I, III e IV, apenas.
I, II, III, IV.

7,82.
4,92.
6,42.
6,87.
8,22.
Em uma equação de regressão envolvendo 30 observações, foi obtida a seguinte equação de regressão estimada:
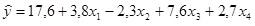
Qual o valor estimado de y quando x1 = 10, x2 = 5, x3 = 1 e x4 = 2? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
80,20.
32,40.
102,30.
48,90.
57,10.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 459.
O gerente de recursos humanos de uma empresa de tecnologia da informação reuniu dados sobre as notas obtidas nos programas de treinamento e salários mensais dos colaboradores. Foi estimada a equação de regressão
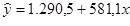
em que x = salários mensais; y = média das notas, encontrando-se os seguintes valores:
Coeficiente de determinação r2 = 0,746;
Fcrítico = 5,96
Fteste = 11,7.
A respeito desse modelo, julgue as seguintes afirmações:
I. Os salários mensais são a variável explicativa e as notas são a variável explicada.
II. As notas obtidas no programa de treinamento explicam 74,6% das variações observadas nos salários mensais.
III. No teste de hipóteses sobre a validade do modelo, rejeita-se a hipótese nula e conclui-se que as notas explicam os salários mensais.
IV. Para cada 1 ponto adicional nos salários mensais, espera-se um acréscimo de R$ 581,10 nas médias das notas.
Estão corretas as afirmações:
II, III e IV, apenas.
I e IV, apenas.
I, II e III, apenas.
I, III e IV, apenas.
I, II, III, IV.

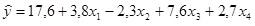
80,20.
32,40.
102,30.
48,90.
57,10.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 459.
O gerente de recursos humanos de uma empresa de tecnologia da informação reuniu dados sobre as notas obtidas nos programas de treinamento e salários mensais dos colaboradores. Foi estimada a equação de regressão
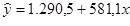
em que x = salários mensais; y = média das notas, encontrando-se os seguintes valores:
Coeficiente de determinação r2 = 0,746;
Fcrítico = 5,96
Fteste = 11,7.
A respeito desse modelo, julgue as seguintes afirmações:
I. Os salários mensais são a variável explicativa e as notas são a variável explicada.
II. As notas obtidas no programa de treinamento explicam 74,6% das variações observadas nos salários mensais.
III. No teste de hipóteses sobre a validade do modelo, rejeita-se a hipótese nula e conclui-se que as notas explicam os salários mensais.
IV. Para cada 1 ponto adicional nos salários mensais, espera-se um acréscimo de R$ 581,10 nas médias das notas.
Estão corretas as afirmações:
II, III e IV, apenas.
I e IV, apenas.
I, II e III, apenas.
I, III e IV, apenas.
I, II, III, IV.

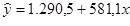
II, III e IV, apenas.
I e IV, apenas.
I, II e III, apenas.
I, III e IV, apenas.
I, II, III, IV.
